The Yield Curve is a Policy Choice

The Federal Reserve Controls Short Term Interest Rates, Expected Future Interest Rates, Term Premium, and Liquidity Premium. QED the Yield Curve is a Policy Choice.

The views expressed in this blog are entirely my own and do not necessarily represent the views of the Bureau of Labor Statistics or the United States Government.

The Federal Reserve directly sets short term nominal interest rates. This is considered a “normal” monetary policy action.

The Federal Reserve can—but chooses not to—directly set long term nominal interest rates. This is considered an “abnormal” monetary policy action dubbed Yield Curve Control (YCC). Instead the Federal Reserve currently chooses to let longer term interest rates (as measured by government bond yields) fluctuate based on expected future interest rates and bond risk premiums. The Federal Reserve has engaged in YCC before—during World War Two—but the policy has remained unused during peacetime.

What was once abnormal, however, is increasingly becoming normal. Ever since Bank of Japan introduced YCC in 2016, other central banks have been exploring the policy. The Reserve Bank of Australia recently followed in Bank of Japan’s footsteps and introduced a 0.25% target rate on three-year bonds in response to the COVID-19 pandemic. With “unconventional” policies like YCC becoming more common it’s critical to understand the central bank’s ability to affect long term interest rates.

While YCC itself may be an abnormal policy, the Federal Reserve’s control of the yield curve is not. The Federal Reserve has unlimited power to set short term interest rates and, if perfectly credible, expected future short term rates. With these tools alongside its unlimited ability to set liquidity premiums through market operations, the Federal Reserve effectively controls expected future interest rates and bonds’ risk premium. Therefore, the yield curve itself is a policy choice.

At Any Rate

Before moving forward, it is important to understand what determines a bond’s yield. Bond yields can be decomposed into expected short term interest rates and the bond’s risk premium. Expected short term interest rates are fairly simple to understand—they are the current and future interest rate on liquid “base money” like bank reserves, the digital cash that commercial banks use to settle transactions. When an investor purchases a bond they are locking in an interest rate until the bonds’ maturity, so they will not accept an interest rate less than they would expect to receive by leaving their money in the highest interest-bearing savings account they could access. That is unless the bonds are less risky than the savings account, which we will discuss more shortly. For the same reason, a bank will not hold Treasury bonds that will yield less than what they expect to earn from interest on their reserves.

Before the introduction of Interest on Excess Reserves (IOER) and Interest on Required Reserves (IORR), the Federal Reserve would set short term interest rates through the quantity of reserves, buying short term government debt with newly created reserves to lower interest rates and vice-versa to raise rates. Nowadays they dictate short term interest rates by simply using IOER and IORR to set a “floor” on interest rates alongside a “subfloor” set by the Overnight Reverse Repurchase Agreement Facility (ONRRP). ONRRP was created to manage the “leaky floor” of IOER whereby interest rates on Treasury bills would constantly sink below IOER because of the dearth of institutions with access to IOER. The same “leaky floor” plagues ONRRP, but through the combination of ONRRP and IOER the Federal Reserve puts a general floor on interest rates. If the Federal Reserve also controls the expected future interest rate through expected future IOER and ONRRP policy.

The risk premium is the second part of a bond’s yield. Treasury bonds generally have extremely little default risk as the Federal Reserve and federal government coordinate to preserve the full faith and credit of the United States. The main exception to this is as the US approaches the debt ceiling, where a risk of default due to legislative gridlock becomes priced in to Treasury bonds. For the purposes of this analysis, it is best to assume that government debt is perfectly risk-free and perfectly backed by the government. Therefore there is no default risk premium. So where does the risk premium on government bonds come from?

Duration and liquidity risk. Duration is a bond price’s sensitivity to changes in interest rates. If 10 year bond yields were 1% and short term interest rates jumped to 2%, the price of the 10 year bonds with 1% yield would drop. In general, longer maturity bonds have higher duration which is why yields on longer maturity bonds tend to be higher to compensate for duration risk. Liquidity risk, the risk that an asset cannot be easily converted to cash, is the second primary risk of bonds. In general US government bonds are extremely liquid assets, but certain types of bonds exhibit large liquidity premiums and liquidity in standard bond markets can dry up during times of crisis.

The chart above shows the evolution of the US yield curve since the financial crisis. The curve dropped in the immediate aftermath of the crash, but it took several years for rates on longer maturity bonds to decrease and for the yield curve to “flatten.” This “flattening” of the curve was due to the deliberate policy of Quantitative Easing (QE), where the Federal Reserve purchases large quantities of bonds with newly created reserves in order to lower long term interest rates and increase the quantity of bank deposits and bank reserves.

Quantitative Easing works through two channels: signaling and portfolio balance. Signaling is the simplest channel—by purchasing large amounts of long term government debt (bonds) with short term government debt (bank reserves) the Federal Reserve is making a credible signal that short term interest rates will remain low for the foreseeable future. Investors generally expect the Federal Reserve to taper and possibly unwind their purchases before proceeding with short term interest rate hikes (though tapering is not an absolute prerequisite for rate hikes). Each purchase is therefore a commitment to extending low short term rates for longer.

Portfolio rebalancing is the more complicated channel. Essentially, the Federal Reserve’s purchases of Treasury bonds reduces the bonds’ liquidity and duration risk. Since the Federal Reserve has unlimited ability to purchase bonds with the bank reserves it creates, it can theoretically create a perfectly liquid market for bonds. Through stabilizing the expected future short interest rate, the Federal Reserve can reduce variance in expected interest rates and therefore reduce duration risk. It should be noted that the signaling and portfolio balance channels are not perfectly separate; signaling a lower and more stable future interest rates will lower duration risk in a way akin to the portfolio balance effect.

So have lower expected short interest rates or lower bond risk premiums driven the flattening of the yield curve? In short, a bit of both—but mostly lower expected short term interest rates. The drop in yields during the start of the COVID-19 pandemic was driven almost entirely by lower expected short term interest rates, although the recent spike in yields has been driven by a higher risk premium. Other notable inflection points are in 2011, when the resolution of an intense debt ceiling debate dropped the bond risk premium into negative territory, and in 2013, when the Federal Reserve’s suggestion that they would end QE in preparation for rate hikes triggered a “taper tantrum” that drove risk premiums higher.

Looking at the graph again, you might have one question—why does the bond risk premium go negative? Well, for one, all models are imperfect. Trying to divine aggregate unobservable like expected short term interest rates will always come with some error terms. But there are also a few theoretical reasons why we would expect the risk premium on bonds to be negative, and they mostly surround a negative liquidity premium.

The “leaky floor” of IOER and ONRRP means that interest rates on short term bonds will generally be lower than IOER and sometimes lower than ONRRP. Since a wide variety of investors and institutions cannot access the IOER or ONRRP rates, bonds are therefore “more liquid” at a given interest rate than bank reserves. This is not an standard measure of liquidity, more of an analogy to “ease of universal conversion to short term interest bearing assets.” US bonds experience a similar effect in regards to non-American investors since it is sometimes easier for a foreigner to access US government bonds than to access risk-free US dollar banking. Finally, in the wake of the financial crisis banks have have faced stringent regulatory requirements that essentially pushed them to hold more Treasury bonds, possibly driving their liquidity premium down further. These are all merely my hypotheses, not empirical facts that explain the model’s negative bond risk premium.

It should, however, be abundantly clear by this point that the Federal Reserve controls bonds’ risk premiums and expected future short interest rates through their policy choices. Even though the Federal Reserve currently lets yields on longer maturity bonds “float”, they effectively can set yields wherever they want by controlling expected future interest rates and bond risk premiums.

Yield Curve Control and You

What would happen if Jerome Powell walked out of the next FOMC meeting and said that the Federal Reserve was committed to keeping interest rates at 0% for the next ten years? If this was a perfectly credible statement, meaning that all market participants believed that the Federal Reserve would stick to its stated goal come hell or high water, then yields on all government bonds with a maturity of 10 years or less would drop to near-0. The expected 10 year short interest rate would be zero, and duration risk for bonds under 10 years would also drop to zero. Bond prices would only reflect liquidity risk, which itself could be reduced to zero if the Federal Reserve committed to purchasing government bonds whenever their yields got above 0%.

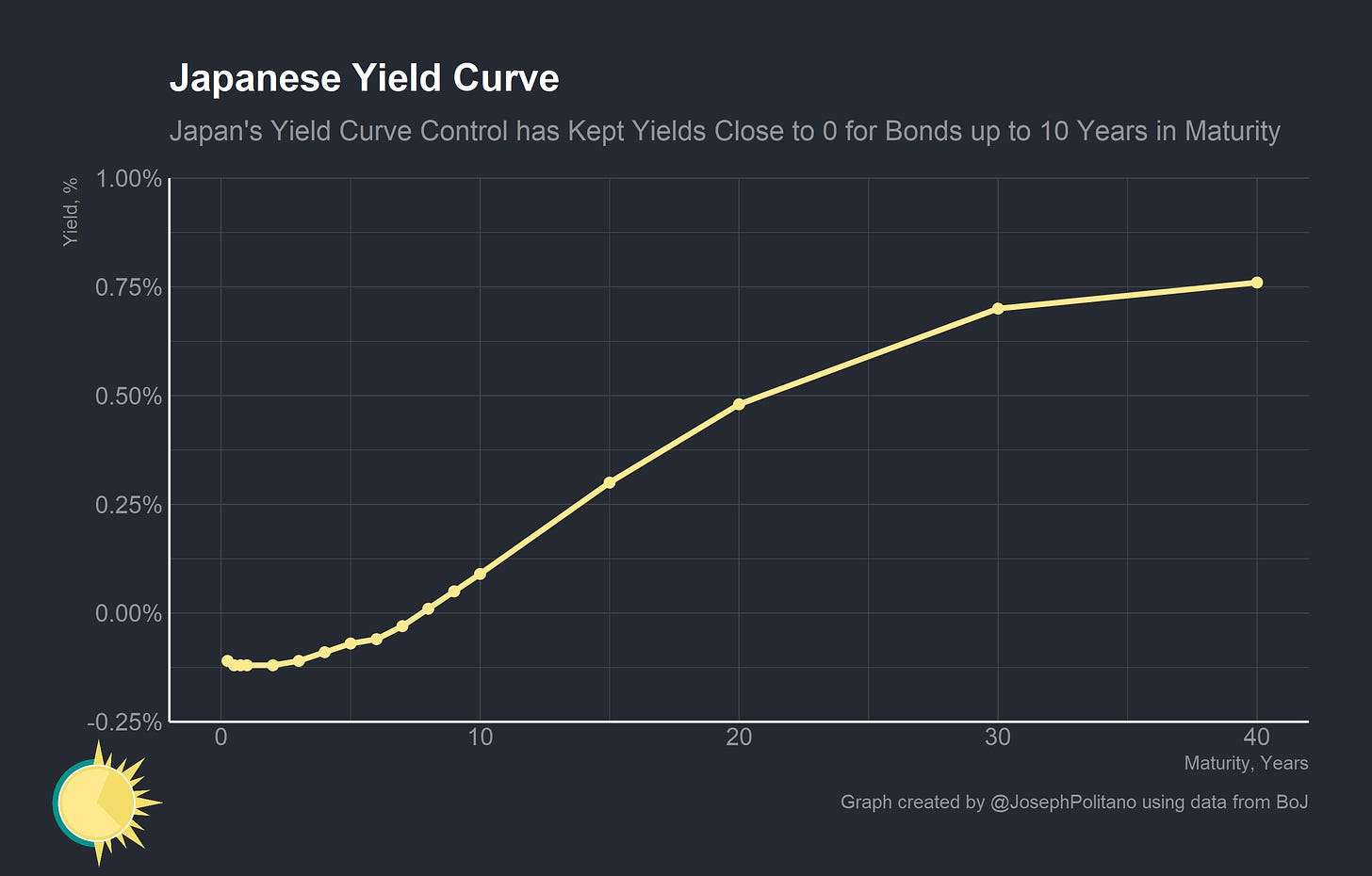
This is effectively what YCC is. Starting in 2016, the Bank of Japan declared that they would not allow yields on 10 year bonds to deviate significantly from 0%. If bond yields began to trend up, the Bank of Japan would simply intervene to purchase bonds in order to drive yields back down. This essentially signals extreme commitment to extremely low interest rates for the next decade, and Bank of Japan has not even had to use a large amount of bond purchases to “enforce” its commitment.

YCC with 0% yield targets essentially converts government bonds to a type of “base money” like cash or bank reserves. Think of it this way—if the central bank guarantees that a $1,000 government bond will always have a 0% interest rate and will always trade for $1,000 on the open market, then that government bond is as good as $1,000 in cash. In cases like Japan, where short term interest rates are actually negative, the 0% government bond is marginally better than reserves and on par with physical cash. Incidentally, this is part of the reason that “base money” as an aggregate concept is flawed—cash, reserves, and bonds can all have similar, but not identical, liquidity and yield properties but cash and reserves are classed together as base money while bonds are not.

It is also worth noting that while QE and YCC can achieve similar reductions in long term interest rates they are not perfectly identical or interchangeable policies. If the central bank is purchasing bonds from non-bank entities through QE, then they are essentially expanding bank balance sheets by increasing bank deposits and bank reserves. YCC does not directly expand bank balance sheets, instead turning bonds into cash-like instruments as discussed before. Central banks could theoretically institute YCC alongside no QE purchases or large QE purchases depending on their desired composition of financial assets in the private sector.

Credibility is perhaps the most important part of successful YCC policy. Investors and private actors must believe that expected future short interest rates will be less than the central bank’s stated yield target for the peg to hold. Imagine if private actors believed that the central bank would back off its YCC policy after one year and instead raise short-term interest rates. YCC policy would break down in such a scenario, and the central bank would be forced to purchase bonds in large quantities in order to re-convince the public that they are serious about YCC. The Reserve Bank of Australia is currently mired in one such fight to preserve its YCC policy. The Federal Reserve has shied away from YCC partly because it worries about building credibility surrounding its interest rate pegs.

Conclusions

So, is YCC a good policy? Well, it is not ideal but it can be useful. If a central bank is pursuing dramatic YCC programs then it has lost the plot in the near past. A successful nominal output target will generally preclude the need for long term interest rate targeting of any kind. In other words, good monetary policy will not need YCC—the yield curve will naturally reflect the expected future short term interest rates needed to preserve nominal output growth alongside duration and liquidity premiums.

YCC is, however, a central part of breaking out of bad monetary policy. In a seminal paper, Paul Krugman argued that central banks facing a liquidity trap where short term interest rates are already at or below 0% must “credibly promise to be irresponsible.” By changing expectations about future monetary policy, central banks can induce increases in current nominal output. What is YCC but a promise from the central bank that they will be “irresponsible” and keep interest rates at super-low levels until nominal output returns to trend and the liquidity trap is defeated?

Even if YCC itself may not be perfect monetary policy, acknowledging that the yield curve is a Federal Reserve policy choice is critical to understanding the bond and credit markets. As one example, take yield curve inversion. The yield curve is usually upward-sloping as shorter maturity bonds have lower yields than longer maturity bonds due to the latter’s greater duration and liquidity risk. When the yield curve inverts short term bonds have a higher interest rate than long term bonds, and this inversion is treated as an indicator of impending recession.

If the yield curve is a policy choice then a yield curve inversion merely indicates that interest rates are expected to drop in the near future, not that a recession is on the way. Yields on short term bonds are higher than on long term bonds because expected interest rates over the short term are higher than expected interest rates over the long term. This likely indicates that monetary policy is too tight and that investors expect the Federal Reserve to have to loosen policy to combat a slowdown in growth, but it does not make yield curve inversion a “cause” or “indicator” of recessions. Incidentally, this is part of the reason why it is important to model the Federal Reserve’s response function when forecasting macroeconomic phenomena.

YCC is also important in highlighting the potential strength of monetary policy. Even when trapped by 0% short term interest rates and political constraints that preclude purchases of stocks or foreign currencies, the Federal Reserve still has tremendous power to alter the trend of nominal growth through YCC. There simply is no excuse for pursuing bad monetary policy that lowers economic growth and employment.

If you liked this post, consider subscribing to get free economics news and analysis delivered to your inbox every Saturday! Leave a comment below to participate in the discussion or share this post to others who may find it useful!